第一学期期中初三数学试题
数 学 试 卷 日期：
（考试时间100分钟，满分150分） 出卷人：
1、选择题（本题大题共6题，每小题4分，满分24分）
1.下列函数中，是二次函数的是（ ）
A、
B、
C、
D、
2.在△ABC中，点D、E分别在边AB、AC上，假如AD:DB=1:3，那样下列条件中可以判断DE∥BC的是（ ）
A、
B、
C、
D、
3.抛物线
与
轴的交点坐标是（ ）
A、（0,1） B、（1,0） C、（0，-1） D、（0,0）
4.一个三角形框架模型的三边长分别为20厘米、30厘米、40厘米，木工要以一根长为60厘米的木条为一边，做一个与模型三角形一样的三角形，那样另两条边的木条长度不符合条件的是（ ）
A、30厘米、45厘米 B、40厘米、80厘米
C、80厘米、120厘米 D、90厘米、120厘米
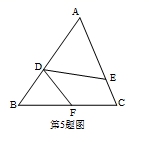
5.如图，在△ABC中，点D、E、F分别在边AB、AC、BC上，且∠AED=∠B，再将下列四个选项中的一个作为条件，未必能使得△ADE∽△BDF的是（ ）
A、
B、
C、
D、
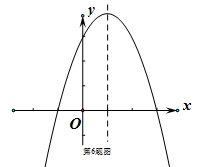
6.已知二次函数
的图像大致如图所示，则下列关系式中成立的是（ ）
A、
B、 C、
D、
2、填空题（本大题共12题，每题4分，满分48分）
7.假如
，那样________.
8.在比率尺是1:15000000的地图上，测得甲乙两地的距离是2厘米，那样甲乙两地的实质距离是________千米.
9.若抛物线
的顶点在
轴上，那样
________.
10.已知线段
，P是AB的黄金分割点，且AP＞BP，那样AB=________.
11.在△ABC中，AB=AC，假如中线BM与高AD相交于点P，那样
________.
12.假如抛物线
的开口向下，那样
的取值范围是________.
13.已知△ABC与△DEF相似，且△ABC与△DEF的相似比为2:3，若△DEF的面积为36，则△ABC的面积等于________.
14.已知点A（-2，
）、B（2，
）都在抛物线
上，则与的大小关系是______.（填“＞”、“＜”或“=”）
15.抛物线
向左平移2个单位长度，得到的新抛物线的表达式为__________.
16.假如二次函数的图像的对称轴是直线
，且在对称轴的右边的部分是上升的，那样这个二次函数的分析式可以是______________________.（写一个即可）
17.假如一条抛物线
与轴有两个交点，那样以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”，请写出“抛物线三角形”是等腰直角三角形且抛物线顶点在轴上时，抛物线的表达式_______________.（写一个即可）
18.在Rt△ABC中，∠C=90°，AB=10，AC=8，点D在斜边AB上，把△ACD沿直线CD翻折，使得点A落在同一平面内的A´处，当A´D∥BC时，AD的长为_______________.
3、解答卷（本大题共7题，满分78分）
19.已知二次函数的图像上部分点的坐标
满足下表：
| … | -2 | -1 | 0 | 1 | … |
| … | 0 | 0 | 2 | 6 | … |
（1）求这个二次函数的分析式，并写出顶点坐标和对称轴；（5分）
（2）若抛物线与轴交点为A、B（A在B的左边），与轴交于点C，顶点为D，顺次联结ADBC，求四边形ADBC的面积.（5分）
20.已知：如图，AB∥CD∥EF，AC、BD相交于点O，E在AC上，F在BD上，且AE:EC=2:3，BD=10.
（1）求BF的长；（5分）
（2）当AB=12，CD=8时，求EF的长.（5分）
21.如图，已知点D是线段BC上的一点，假如添加条件∠DAC=∠ABC，可得到结论：
__________，在划线上填写一个与线段有关的结论并证明.（10分）
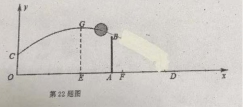
22.如图，已知排球场的长度为18米，坐落于球场中线处球网的高度AB为2.5米，一队员站在点O处发球，排球从点O的正上方2米的C点向正前方飞出，当排球运行至离点O的水平距离OE为7米时，到达最高点G，打造如图所示的平面直角坐标系.
（1）当球上升的最大高度为3米时，求排球飞行的高度（单位：米）与水平距离（单位：米）的函数关系式.（不需要写自变量的取值范围）（5分）
（2）在（1）的条件下，判断这次发球是不是可以过网？请通过计算说明.（5分）
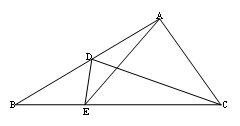
23.已知：如图，在△ABC中，点D、E分别在边AB、AC上，∠BAE=∠BCD.
（1）求证：
；
（2）假如AE=AC，求证：
.
24.（本题满分12分，其中第（1）小题3分，第（2）小题5分，第（3）小题4分）
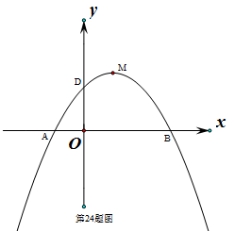
如图，在平面直角坐标系中，O为坐标原点，抛物线与轴交于A、B两点，与轴交于点D，M是抛物线的顶点.
（1）求A、B两点的坐标；
（2）若点D（0,3）时，联结AD、BD、BM，求证：∠ADO=∠DBM；
（3）当△BDM为直角三角形时，求的值.
25.（本题满分14分，第（1）①小题4分，第（2）②小题5分，第（3）小题5分）
如图，如图，已知梯形ABCD中，AD∥BC，AB=CD=8，∠ABC=60°，E是AB边上的一点，且
，点F是射线BC上一点，连接EF，射线EF交射线DC于点G.
（1）当F与C重合时；
①联结DE，当
时，求出△ADE与△BEC的面积之比；
②当∠ADE=∠DCE，试求线段DE的长.
（2）设，
，且AD=8，求与的函数关系式，并写出概念域.
教师评语：
教师签名：__________ |
